Spin it as you like !

Now that you have looked at different factors that affect the rotation of the cores of star, let's have a look at what kind of final spin we would expect for the compact object! To measure the spin of a black hole, we can use the dimensionless spin parameter $a$ which is defined as:

$$ a = \frac{J}{J_{max}} $$ whith J the angular momentum of the core, and $J_{max}$ the maximum angular momentum $J_{max}$ that a Kerr black hole of that mass can have: $$ J_{max}(M) = \frac{GM^2}{c} $$ so that $$ a = j \frac{c}{GM} $$ with $j$ the specific angular momentum, $c$ the speed of light, $G$ the gravitational constant and $M$ the mass.

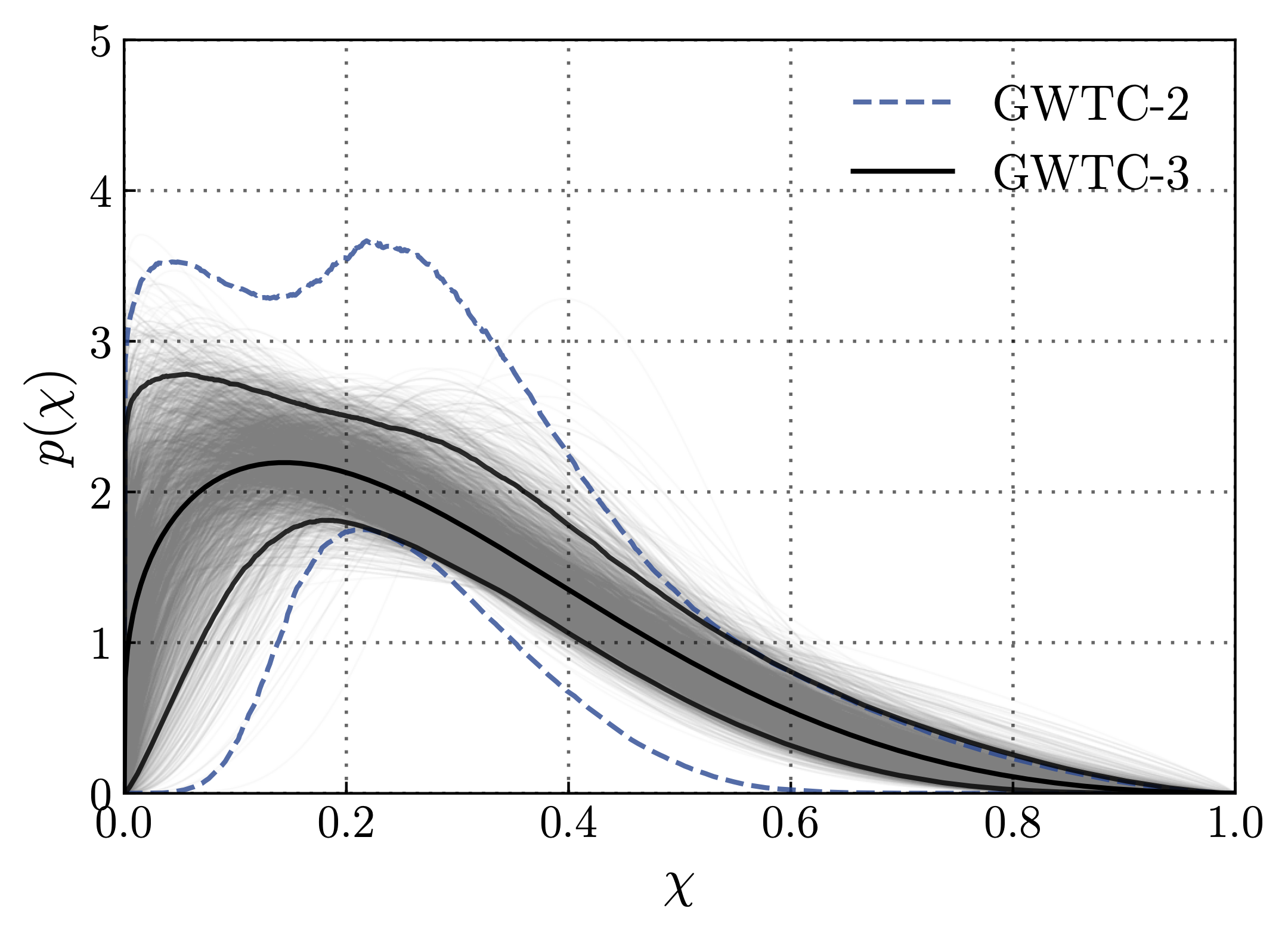
The LIGO-Virgo-KAGRA (LVK) collaboration has measured the spins of black holes through gravitational waves. The figure below shows the distributions of the component spin magnitudes of black holes measured from the most recent catalog, gravitational-wave transient catalog 3 (GWTC-3).

We see that most black holes are slowly spinning, but they don't have a spin of zero. Most black holes have a spin parameter $a$ of around 0.1.

Final project

With your group of 3 fellow participants, calculate the final dimensionless spin of a compact object for different initial conditions.

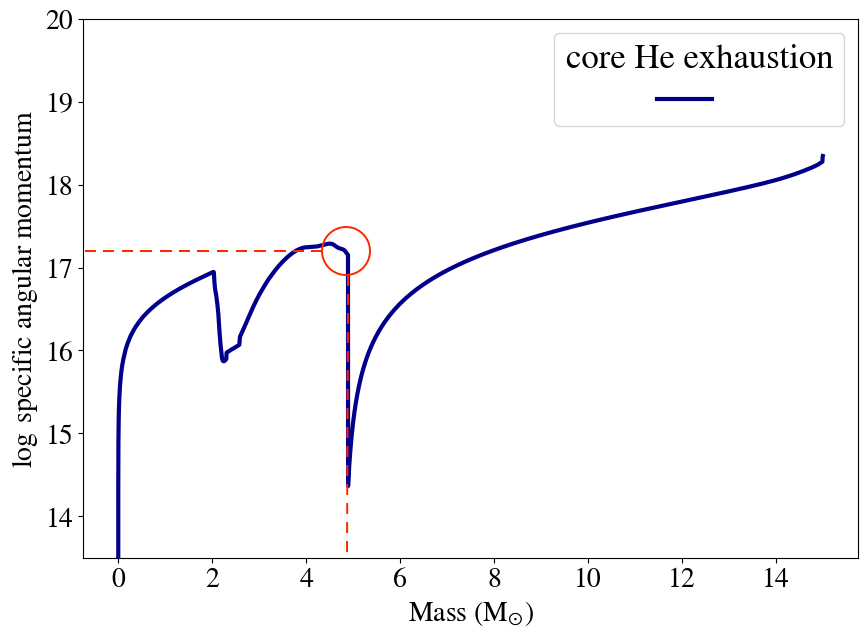
Use the mass of the core and the specific angular momentum at core He-exhaustion as your input parameters. To retrieve those values, use the value at the core-envelope boundary of your j-profiles as shown in the example plot below:

• Can you get a black hole with a spin that looks like the GW-detected black holes?

Vary your initial rotation between $10\% - 60\%$ of critical rotation, the constant mass-loss rate $ < 5 \cdot 10^{-7} \mathrm{M_{\odot}/yr}$, and turn the Tayler-Spruit dynamo on and off.
Warning: if you deviate much from these values there is a good chance that that the simulation will break!

• Work with your group to prepare a 5-minute presentation on your results.

If you didn't get your MESA simulation to run, don't worry. Just explain how you would have varied the different input parameters, focussing in particular on the effect of each parameter on the final spin.

Good luck!

Note that we are making a LOT of over-simplifications here. In relaity, the mapping of the final core mass to the black hole (or neutron star) mass depends on the complex physics of the supernova explosion. Moreover, in the interest of time, we stopped our simulations early (at core He-exhaustion), while the end of Carbon-Oxygen burning would be a much more appropriate time to stop the simulations. But later burning stages take much longer to simulate (can you think of the reason why this is?).